Все модели исходили из того, что атом электронейтрален.

1. Томсон в 1897 году создал первую модель атома.

           

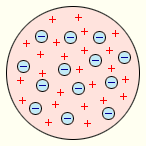
Ø≈10-10 м

 

2. Х. Нагаока в 1903 году представил себе расположение электронов в атоме подобно кольцам Сатурна.
3. Резерфорд в 1911 сформулировал планетарную модель атома. Так в центре находится маленькое, но тяжелое ядро, а легкие электроны расположены на достаточно большом расстоянии от него.

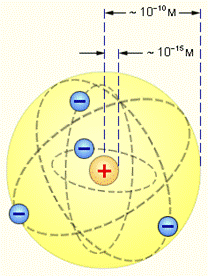
А.     При вращении электрон излучает энергию и должен упасть на ядро. Вывод: атом является неустойчивым, а на самом деле в настоящее время атом является самой устойчивой из известных систем. В этом и есть первое и главное противоречие, если рассматривать атом с точки зрения классической механики.

Б.      Должна непрерывно меняться частота, так как вращение равномерно, но у него непрерывный спектр излучения. Такой спектр  дает вещество в твердом и жидком состоянии, на самом деле атом дает спектр

 

Нильс Бор в 1913 году.

Постулаты:

              I.      Электроны в атоме могут двигаться только по определенным стационарным орбитам, и при этом энергия не излучается (Боровская орбита).

  

            me – масса электрона

            ve – скорость электрона

            rn – радиус орбиты

           

Момент импульса электрона на боровской орбите равен примерно целому числу, причем, n≠0.

           II.      Атом излучает или поглощает квант энергии при переходе электрона из одного энергетического состояния в другое ( с одной орбиты на другую).

hn=E2-E1

E1 – стационарное энергетическое состояние электрона

E2 – энергия электрона в возбужденном состоянии.

Наименьшее энергетическое состояние электрона в атоме – на ближайшей к ядру орбите n=1. Данная формула объяснила линейчатые спектры атома.

 

Спектры электромагнитного излучения атома.

 

 

 

 

 

 

            Радиоволны и радарное излучение в том случае, когда происходит изменение спина атома или ядра. Инфракрасное – за счет колебаний атомов в молекуле. Видимое, ультрафиолетовое – за счет квантовых переходов внешних электронов атома из возбужденного состояния в основное. Рентгеновское – за счет перехода электронов с внешних оболочек на внутренние. Гамма-излучение – связано с ядерными процессами и никак не связана с электронами.

            Теория Бора является промежуточным звеном между классической и квантовой механикой.

            Первый постулат был объяснен на основе уравнений де Бройля.

2πrn – длина окружности боровской орбиты.

Вывод: боровские (стационарные) орбиты – это такие орбиты, на которых укладывается целое число волн де Бройля.

 

Критерии применимости законов микро-, макро- и мегамира.

1.      Макромир: Законы классической механики. Главный критерий: v<<c.

2.      Мегамир: v®c. Релятивистская механика.

3.      Микромир: Квантовая механика – постоянная Планка.

 

Гейзенберг в 1926 году выдвинул принцип неопределенности.

            Для частиц, обладающих корпускулярно-волновым дуализмом нельзя одновременно определить точно и координату и импульс. Чем точнее определяется координата, тем менее точно можно определить импульс.

Δx – это неопределенность, или неточность, нахождения координаты импульса.

Δpx – неопределенность, или неточность нахождения самого импульса.

Если это произведение сравнимо с постоянной Планка, то поведение частицы описывается квантовой механикой. Если это произведение велико, то есть, много больше постоянной Планка, то поведение частицы описывается классической механикой.

            Ни для какого движения в природе это произведение не будет меньше постоянной Планка.

            Одновременное изменение энергии и среднее время жизни возбужденной частицы также нельзя измерить одновременно.

ΔE – средняя ширина энергетического уровня.

В 1926-м году Э. Шредингер вывел фундаментальное уравнение квантовой механики. Вывел волновое уравнение, в которое входит функция Ψ(x, y, z), зависящую от всех трех координат движения электрона и являющуюся аналогом амплитуды. Волновое уравнение Шредингера выведено из уравнения поперечной волны классической физики. Функция, как и амплитуда, может быть положительной и отрицательной.

            Ψ2 представляет наибольший интерес. Квадрат волновой функции имеет определенный физический смысл. Квадрат функции характеризует вероятность нахождения электрона в данной точке атомного пространства с координатами x, y, z. Из уравнения Шредингера следует, что нельзя говорить о какой-то определенной боровской орбите, по которой движется электрон. Более правильно говорить об электронном облаке, а именно, о его наибольшей плотности в каком-то месте атома. И там, где плотность наибольшая, там и есть наибольшая вероятность нахождения данного электрона (ок. 90%). Пространство вокруг ядра, в котором наиболее вероятно находится электрон, называется орбиталью. Эти орбитали и есть решения уравнения Шредингера. Эти решения характеризуются тремя константами, которые Шредингер называл квантовыми числами n, l, m.

            n – главное квантовое число, которое определяет размер атома (n от 1 до бесконечности) и показывает энергетический уровень электрона в атоме. Чем больше n, тем более высокой энергией обладает электрон. Если n>>1, то энергетический уровень образует не дискретный спектр, а сплошной, то есть, это уже объект макромира.

 

Принцип соответствия Бора: Законы квантовой механики при больших значениях квантовых чисел переходят в законы классической механики.

            Вывод из этого принципа: всякая новая теория является развитием предыдущих теорий и полностью её не отвергает, а лишь указывает границы её применимости.

            l – орбитальное (побочное или азимутальное) квантовое число. Характеризует  (показывает) форму электронного облака и изменяется от 0 до (n-1), то есть, зависит от главного квантового числа. l определяет значение момента количества движения электрона по орбите.

           

            l характеризует число подуровней на заданном энергетическом уровне.

            Каждому значению l соответствует орбиталь особой формы.

            Орбитали с l = 0 называются s-орбиталями,

            l =1 - р-орбиталями (3 типа, отличающихся магнитным квантовым числом m),

            l = 2 - d-орбиталями (5 типов),

            l = 3 - f-орбиталями (7 типов).

 

            m – магнитное квантовое число. Показывает ориентацию электронного облака в атоме при взаимодействии магнитного поля электрона с внешним магнитным полем и магнитными полями соседних электронов. m определяет число орбиталей на данном подуровне l (от –l до +l).

 

n=1	l=0(s)	m=1
n=2	l=0(s), 1(p)	m=1,3 m=-1,0,1
n=3	l=0(s),1(p),2(d)	m=1,3,5

 

            Три квантовых числа n, l и m определяют волновые свойства электрона (следует из решения уравнения Шредингера).

            s – квантовое число, называемое спин.

           

            Частица с целым спином.

 

Принцип Паули: В атоме не может быть электронов, у которых все квантовые числа равны. Это связано с тождественностью частиц. В атоме не может быть двух электронов в одинаковых энергетических состояниях.

 

Принцип дополнительности Бора (сформулирован в 1927-м году): Получение экспериментальной информации об одних физических величинах, описывающих частицу, неизбежно связано с потерей информации о других величинах, дополнительных к первой.

            Eкин ® Епот

            v®(x,y,z)

            С точки зрения физика-экспериментатора это связано с влиянием макроприбора на микроскопический объект. С точки зрения квантовой механики определить одновременно основные свойства частицы и дополнительные к ним невозможно точно ни на каком приборе, так как частицы обладают корпускулярно-волновым дуализмом.

 

Принцип неопределенности Гейзенберга: увеличение точности определения положения частицы вызывает увеличение ошибки определения ее момента (энергии), если эти определения проводятся одновременно.

 

Принцип причинности (Связан с Лапласовским детерминизмом): Если мы знаем исходное условие (причину), то всегда можем определить следствие.

            Квантовая механика основывается на теории вероятностей.

Ψ0®|Ψ|2 – Квадрат функции показывает наибольшую вероятность местоположения данной частицы.

 

• Современная концепция атомного ядра.
• Фундаментальные взаимодействия.
• Концепция молекулярно-кинетического взаимодействия (макромир).
• Идеальный газ.
• Основные газовые законы для идеальных газов.
• Основные законы классической (равновесной термодинамики).
• Концепции эволюции реальных систем.
• Концепции космологии.